题目：

给定一个非负索引 index，返回杨辉三角的第 index 行

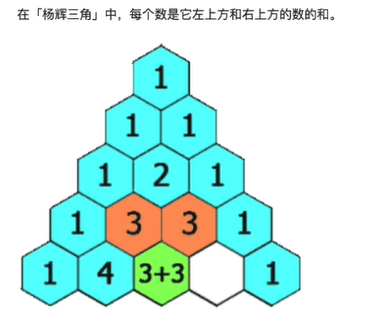
在杨辉三角中，每个数是它左上和右上的和。

首先考虑，用什么数据结构来存储杨辉三角，

首选用一个矩阵，也就是二维数组

如下图：

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

其他的位置，用0来填充

1 0 0 0 0

1 1 0 0 0

1 2 1 0 0

1 3 3 1 0

1 4 6 4 1

这样我们就用了一个二维数组，来存储了杨辉三角

行从0开始，0行有1个元素，第n行有n+1个元素

代码如下：

#include <bits/stdc++.h> 
using namespace std;
int f[34][34];
int r[34];
int main(){
    int n;cin>>n;
    for(int i=0;i<=n;i++) {//从0行到n行 
        //第i行，有i+1个元素 所以j从0->i，共i+1次 
        for(int j=0;j<=i;j++) {
            if(j==0 || j==i) { //当处于矩阵最左边，或者对角线 
                f[i][j] = 1;   // 杨辉三角的边界 
            }else{
                //上一行同列 + 上一行前列 
                f[i][j] = f[i-1][j] + f[i-1][j-1];
            }     
        }
    }

    for(int i=0;i<=n;i++) { //第n行，0列->n列 
        r[i] = f[n][i] ;
    }
    for(int i=0;i<=n;i++) {
        cout << r[i] << " ";
    }

    return 0;
}